sklearn实现支持向量机(异常检测)

💥 项目专栏:sklearn实现经典机器学习算法(附代码+原理介绍)
前言
🌟 哈喽,亲爱的小伙伴们,你们知道吗?最近我们的粉丝群里有好多小可爱私信问我一些关于决策树、逻辑回归等机器学习的超级有趣的问题呢!🌈 为了让大家更轻松地理解,我决定开一个超可爱的专栏,叫做 用sklearn玩转机器学习,特别适合机器学习的小新手哦!
🍬 在这个专栏里,我们会用sklearn这个超级强大的魔法工具来实现各种闪闪发光的机器学习算法!不用担心难度哦,我会用最简单、最可爱的方式,带领大家一起探索算法的神秘世界!✨
🎈 适合哪些小伙伴加入呢?当然是对机器学习感兴趣的小新手们,还有那些刚开始接触sklearn的可爱宝宝们!我们会一起学习如何用sklearn轻松实现那些看起来好厉害的机器学习算法,让新手小白也能快快乐乐地理解它们哦!
🌸 在这个专栏里,大家可以看到用sklearn实现的机器学习算法,我们不仅仅是理论学习哦,每一篇文章都会附带 完整的代码+超级可爱的原理讲解,让大家在轻松愉快的氛围中一起学习成长呢!🌼 快来加入我们的学习大冒险吧!
🚨 我的项目环境:
- 平台:Windows11
- 语言环境:Python 3.10
- 编译器:Jupyter Lab、PyCharm
- scikit-learn:1.2.1
- Pandas:1.3.5
- Numpy:1.19.3
- Scipy:1.7.3
- Matplotlib:3.1.3
💥 项目专栏:sklearn实现经典机器学习算法(附代码+原理介绍)
一、算法背景
支持向量机(SVM)在异常检测领域的应用主要是通过一种特殊形式的SVM实现的,即单类支持向量机(One-Class SVM)。这种方法的核心思想是基于数据集找出一个决策边界,这个边界尽可能地包含所有正常数据点(inliers),同时排除异常数据点(outliers)。下面是One-Class SVM在异常检测中应用的一些关键点:
1. 算法背景:
基本原理:
- 单类分类:与传统的SVM不同,One-Class SVM专注于单一类别的数据。它的目标是找到一个最佳边界,这个边界围绕着数据空间中的正常点,而将异常点排除在外。
- 特征空间映射:One-Class SVM利用核技巧将数据映射到高维特征空间,在这个空间中寻找最优的边界来分隔正常点和异常点。
核函数:
- 核函数用于处理非线性可分的数据。常见的核函数包括线性核、多项式核、径向基函数(RBF)核等。核函数的选择对算法的性能有显著影响。
2. 异常检测:
决策函数:
- One-Class SVM的决策函数基于数据点与决策边界的距离。这个距离用于判断一个新的观测点是正常点还是异常点。
超参数:
- ν(nu):这个参数是One-Class SVM中的关键参数,它控制着模型的敏感度。ν是一个介于0到1之间的值,代表异常点所占的比例上限和支持向量所占的比例下限。
- γ(gamma):当使用RBF核时,γ参数定义了单个训练样本影响的
范围。较大的γ值意味着更近的点有更大的影响,这可能导致过拟合;而较小的γ值意味着更远的点也会影响决策边界,这可能导致欠拟合。
3. 算法优势与局限性:
优势:
- 适用于非线性数据:通过使用核函数,One-Class SVM可以有效处理非线性可分的数据集。
- 适用于高维数据:SVM在高维空间中表现良好,尤其适合于特征维数高于样本数的情况。
- 灵活性:通过调整核函数和超参数,可以适应不同的数据分布和异常检测需求。
局限性:
- 参数选择敏感:ν和γ等超参数的选择对模型性能有很大影响,但在没有标签数据的情况下很难选择最优参数。
- 计算成本:尤其是在大数据集上,One-Class SVM的训练可能非常耗时。
- 对异常点敏感:One-Class SVM可能对训练数据中的异常点敏感,这可能导致模型过度适应这些点。
4. 应用场景:
One-Class SVM通常用于如下场景:
- 新颖性检测:在训练时只有正常数据可用,目的是检测新的异常样本。
- 异常检测:在复杂数据集中识别异常或离群值,尤其是在无法明确界定正常和异常数据分布的情况下。
5. 实践中的考虑:
在实际应用中,需要综合考虑数据的特性、可用资源以及特定需求来决定是否使用One-Class SVM以及如何调整其参数。通常,需要通过交叉验证、网格搜索等方法来优化参数选择。同时,对于大型数据集,可能需要考虑使用更高效的算法或使用技术如随机梯度下降来降低计算成本。
二、算法原理
支持向量机(SVM)在异常检测中通常采用其特殊形式——单类支持向量机(One-Class SVM)。这种方法基于寻找数据中的正常模式,并尽可能排除异常点。下面是单类支持向量机在异常检测中的算法原理:
1. 基本概念:
单类支持向量机的核心思想是找到一个最小的超球体,它可以包含数据集中的大部分(或者一个指定比例的)正常点,同时将异常点排除在外。
2. 数据映射:
由于原始数据空间中的点可能不是线性可分的,单类SVM使用核技巧将数据映射到一个更高维的空间。在这个空间中,数据点更有可能是线性可分的,从而使算法能够找到一个能够包围大部分数据点的超球体。
3. 目标函数和优化:
单类SVM的目标是最大化超球体的体积,同时确保大部分数据点都在超球体内。这可以通过以下优化问题实现:
- 最小化:超球体的半径的平方,以及一个松弛变量(用于处理异常点)的总和。
- 约束条件:确保数据点要么在超球体内部,要么在松弛范围内。
4. 核函数:
单类SVM通常使用核函数来处理非线性数据。常见的核函数包括:
- 线性核:用于线性可分的数据。
- 径向基函数(RBF)核:能够处理非线性关系。
- 多项式核:另一种处理非线性关系的方法。
5. 参数选择:
单类SVM的性能高度依赖于参数的选择,主要包括:
- ν(nu):这是一个介于0和1之间的参数,代表异常点(或支持向量)所占的最大比例。较小的ν值使模型更严格,只允许少数异常点。
- γ(gamma):仅在使用RBF核时相关,它决定了单个数据点影响的范围。较高的γ值会导致更紧密的边界。
6. 异常检测:
一旦模型被训练,它可以被用来评估新的数据点是否为异常。如果一个点位于超球体之外,则被视为异常。
7. 应用和局限性:
-
应用:单类SVM非常适用于“新颖性检测”场景,其中在训练阶段只有正常数据可用,目标是识别在操作环境中出现的任何异常或新奇模式。它也用于检测工业系统中的故障、金融领域中的欺诈行为以及在网络安全中识别入侵等场景。
-
局限性:单类SVM的主要限制之一是它的计算复杂性,特别是在处理大型数据集时。此外,它对参数选择非常敏感,错误的参数设置可能导致模型性能不佳。此外,如果训练数据中包含异常点,这可能会影响模型的准确性。
8. 算法原理的数学表达:
设 X = { x 1 , x 2 , . . . , x n } X = \{x_1, x_2, ..., x_n\} X={x1,x2,...,xn} 是训练数据集,单类SVM的目标是找到一个函数 f ( x ) f(x) f(x),使得对于大多数 x i x_i xi,有 f ( x i ) ≥ 0 f(x_i) \geq 0 f(xi)≥0。这个函数的形式通常是:
f ( x ) = sign ( w ⋅ ϕ ( x ) − ρ ) f(x) = \text{sign}(w \cdot \phi(x) - \rho) f(x)=sign(w⋅ϕ(x)−ρ)
其中, w w w 是正常数据的特征向量, ϕ ( x ) \phi(x) ϕ(x) 是将数据映射到高维空间的函数, ρ \rho ρ 是决策边界的偏移量。
优化目标是最小化 ∥ w ∥ 2 \|w\|^2 ∥w∥2 和松弛变量的总和,同时确保大部分的 x i x_i xi 满足 w ⋅ ϕ ( x i ) ≥ ρ w \cdot \phi(x_i) \geq \rho w⋅ϕ(xi)≥ρ。
9. 实际应用注意事项:
在实际应用中,很重要的一点是通过交叉验证或其他方法合理选择核函数和参数(如 ν \nu ν 和 γ \gamma γ)。此外,对于大型数据集,可能需要采用更高效的实现或使用基于近似方法的变体,如使用随机梯度下降的SGDOneClassSVM。
三、算法实现
3.1 导包
import time
import matplotlib.pyplot as plt
import numpy as np
from sklearn import svm
from sklearn.covariance import EllipticEnvelope
from sklearn.datasets import make_blobs, make_moons
from sklearn.ensemble import IsolationForest
from sklearn.kernel_approximation import Nystroem
from sklearn.linear_model import SGDOneClassSVM
from sklearn.neighbors import LocalOutlierFactor
from sklearn.pipeline import make_pipeline
3.2 加载数据集
这段代码的作用是创建用于异常检测算法测试的多个合成数据集。具体来说:
-
示例设置:
- 定义了总共300个样本。
- 设定了异常值的比例为15%,据此计算出异常值和正常值的数量。
-
数据集定义:
- 使用
make_blobs和make_moons函数生成不同特性的合成数据集。 - 第一个数据集:中心位于(0, 0),标准差为0.5,创建了一个标准的、紧密的点群。
- 第二个和第三个数据集:分别创建了两个中心点在(2, 2)和(-2, -2)的点群,但标准差不同(分别为0.5和[1.5, 0.3]),生成了形状和密度不同的数据群。
- 第四个数据集:利用
make_moons函数生成了两个交叠的月牙形数据群,这对于测试算法在处理有特定形状的数据集时的能力很有用。 - 第五个数据集:随机生成了均匀分布的点,范围在一个大的区域内,用于测试算法在处理均匀分布数据时的性能。
- 使用
这些数据集被设计用来评估和比较不同的异常检测算法在处理不同类型的数据时的性能,如密集点群、具有特定几何形状的数据,以及均匀分布的数据。
# 示例设置
n_samples = 300 # 样本总数
outliers_fraction = 0.15 # 异常值比例
n_outliers = int(outliers_fraction * n_samples) # 异常值数量
n_inliers = n_samples - n_outliers # 正常值数量
# 定义数据集
blobs_params = dict(random_state=0, n_samples=n_inliers, n_features=2)
datasets = [
make_blobs(centers=[[0, 0], [0, 0]], cluster_std=0.5, **blobs_params)[0],
make_blobs(centers=[[2, 2], [-2, -2]], cluster_std=[0.5, 0.5], **blobs_params)[0],
make_blobs(centers=[[2, 2], [-2, -2]], cluster_std=[1.5, 0.3], **blobs_params)[0],
4 * (make_moons(n_samples=n_samples, noise=0.05, random_state=0)[0] - np.array([0.5, 0.25])),
14 * (np.random.RandomState(42).rand(n_samples, 2) - 0.5)
]
3.3 定义模型
这段代码定义了一组用于比较的异常检测方法。每种方法都是为了识别和分离数据集中的异常值(即离群值)。具体来说:
-
鲁棒协方差 (EllipticEnvelope):
- 这种方法基于假设正常数据遵循高斯分布(椭圆分布)。
- 使用
contamination参数来估计数据集中异常值的比例。 - 在二维数据上特别有效,适用于检测远离正常数据群体中心的异常点。
-
单类SVM (OneClassSVM):
- 这种方法使用单类支持向量机来识别异常值。
nu参数指定了训练集中异常点的预期比例。- 使用径向基函数(RBF)核和
gamma参数来控制决策边界的形状。
-
单类SVM (SGD):
- 这是单类SVM的一种变体,使用随机梯度下降(SGD)进行优化。
- 结合了核近似(Nystroem方法)来处理大规模数据集。
- 适用于需要处理大量数据或需要更快计算速度的场景。
-
隔离森林 (IsolationForest):
- 该方法基于随机森林,通过隔离异常点而非构造正常点的表示。
contamination参数用于估计数据集中的异常比例。- 适合处理高维数据和大规模数据集。
-
局部异常因子 (LocalOutlierFactor):
- 这种方法考虑了数据点相对于其邻居的局部密度偏差。
- 通过比较给定点和其邻居的局部密度,识别密度显著低于其邻居的点作为异常。
n_neighbors用于指定用于估计局部密度的邻居数量。
这些方法各有特点,适用于不同的数据类型和场景。在实际应用中,选择哪种方法取决于数据的特性、问题的特定需求以及性能要求。
# 定义用于比较的异常检测方法
anomaly_algorithms = [
("鲁棒协方差", EllipticEnvelope(contamination=outliers_fraction, random_state=42)),
("单类SVM", svm.OneClassSVM(nu=outliers_fraction, kernel="rbf", gamma=0.1)),
("单类SVM (SGD)", make_pipeline(
Nystroem(gamma=0.1, random_state=42, n_components=150),
SGDOneClassSVM(nu=outliers_fraction, shuffle=True, fit_intercept=True, random_state=42, tol=1e-6)
)),
("隔离森林", IsolationForest(contamination=outliers_fraction, random_state=42)),
("局部异常因子", LocalOutlierFactor(n_neighbors=35, contamination=outliers_fraction))
]
这些异常检测模型的主要参数。
1. 鲁棒协方差 (EllipticEnvelope)
| 参数 | 描述 | 可选的值/类型 |
|---|---|---|
contamination | 数据集中异常值的比例估计。 | 浮点数(0到1之间) |
random_state | 随机数生成器的种子。 | 整数或None |
support_fraction | 用于估计协方差矩阵的数据点比例。 | 浮点数(0到1之间) |
store_precision | 是否存储精确的逆协方差矩阵。 | 布尔值 |
assume_centered | 是否假设数据已居中。如果为True,将不会计算数据中心。 | 布尔值 |
2. 单类SVM (OneClassSVM)
| 参数 | 描述 | 可选的值/类型 |
|---|---|---|
nu | 异常样本比例的上界和支持向量的下界。 | 浮点数(0到1之间) |
kernel | 核函数类型。 | ‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’ |
gamma | 核函数的系数(仅对‘rbf’, ‘poly’和‘simgoid’有效)。 | 正浮点数、‘scale’、‘auto’ |
degree | 多项式核的次数(仅对‘poly’核有效)。 | 正整数 |
coef0 | 核函数的独立项(仅对‘poly’和‘simgoid’核有效)。 | 浮点数 |
tol | 收敛容忍度。 | 正浮点数 |
shrinking | 是否使用收缩启发式。 | 布尔值 |
cache_size | 内核缓存大小(MB)。 | 正浮点数 |
max_iter | 最大迭代次数。 | 正整数或-1(无限制) |
3. 单类SVM (SGD)
| 参数 | 描述 | 可选的值/类型 |
|---|---|---|
nu | 异常样本比例的上界。 | 浮点数(0到1之间) |
shuffle | 在每次迭代时是否打乱数据顺序。 | 布尔值 |
fit_intercept | 是否计算截距。 | 布尔值 |
random_state | 随机数生成器的种子。 | 整数或None |
tol | 停止迭代的容忍度。 | 正浮点数 |
max_iter | 最大迭代次数。 | 正整数 |
n_components | Nystroem核近似的组件数。 | 正整数 |
gamma | Nystroem核函数的系数(仅对‘rbf’, ‘poly’和‘simgoid’有效)。 | 正浮点数、‘scale’、‘auto’ |
4. 隔离森林 (IsolationForest)
| 参数 | 描述 | 可选的值/类型 |
|---|---|---|
contamination | 数据集中异常值的比例估计。 | 浮点数(0到0.5之间)、‘auto’ |
random_state | 随机数生成器的种子。 | 整数或None |
n_estimators | 构建的树的数量。 | 正整数 |
max_samples | 用于训练每棵树的样本数量。 | 正整数或浮点数(0到1之间) |
max_features | 每棵树的最大特征数量。 | 正整数 |
bootstrap | 是否对样本进行自助采样。 | 布尔值 |
n_jobs | 并行运行的任务数。 | 正整数或None |
5. 局部异常因子 (LocalOutlierFactor)
| 参数 | 描述 | 可选的值/类型 |
|---|---|---|
n_neighbors | 用于估计局部密度的邻居数量。 | 正整数 |
contamination | 数据集中异常值的比例估计。 | 浮点数(0到0.5之间)、‘auto’ |
metric | 计算邻居间距离的方式。 | 字符串(例如 ‘euclidean’, ‘manhattan’, ‘minkowski’, 等) |
algorithm | 用于计算最近邻居的算法。 | ‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’ |
leaf_size | 传递给‘ball_tree’或‘kd_tree’的叶大小。 | 正整数 |
p | Minkowski距离的幂参数(仅在metric='minkowski’时使用)。 | 正整数 |
novelty | 是否用于新颖性检测(在未见过的新数据上进行预测)。 | 布尔值 |
n_jobs | 并行运行的任务数。 | 正整数或None |
这些参数为每种异常检测方法提供了不同的配置选项,使它们可以根据特定的数据特征和应用场景进行调整。理解和合理设置这些参数对于优化模型性能和提高异常检测的准确性至关重要。
3.4 可视化异常检测算法
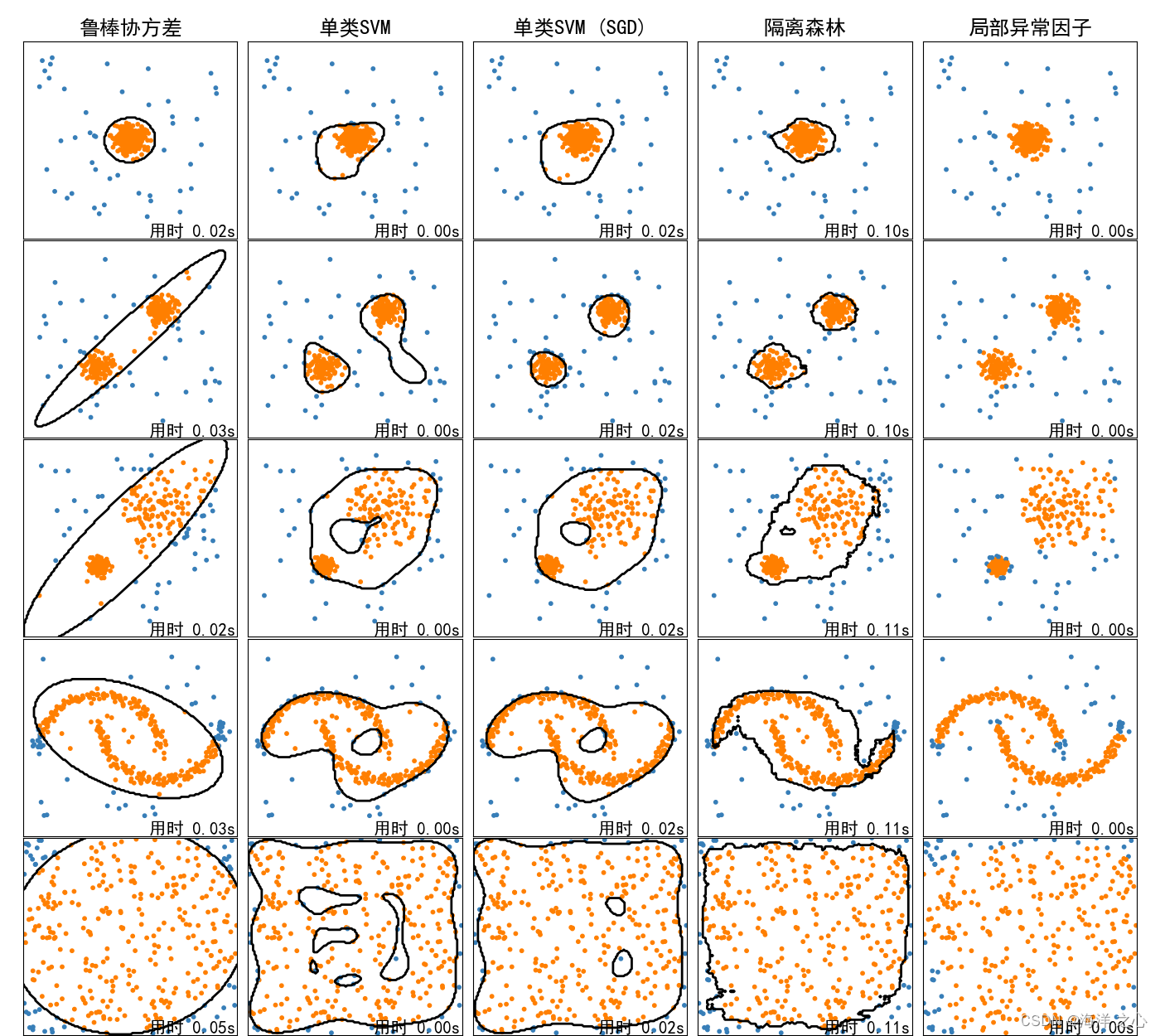
这段代码的目的是为了可视化不同异常检测算法在多个合成数据集上的性能。具体步骤如下:
-
绘图网格设置:首先,它创建了一个网格(
xx,yy),这个网格用于绘制异常检测的决策边界。 -
创建绘图窗口:接着,代码设置了一个绘图窗口,并根据异常检测算法的数量调整窗口大小。
-
数据集处理:对于每个预先定义的数据集,代码会添加一些随机生成的异常值。
-
算法应用与计时:每种异常检测算法都应用于扩展后的数据集,并记录算法拟合数据所需的时间。
-
绘制结果:对于每种算法和数据集的组合,代码绘制了数据点和决策边界。对于支持
predict方法的算法,使用等高线来表示决策边界。每个点根据其被算法判定为正常或异常的预测结果着色。 -
布局调整和显示:最后,代码调整了每个子图的布局,并在图的右下角显示了算法拟合所用的时间。完成所有绘图后,通过
plt.show()展示最终的可视化结果。
这段代码是一种直观展示不同异常检测算法如何在不同类型的数据集上工作的有效方法,可以清楚地看到每种算法对于正常和异常数据点的分类情况,以及其决策边界的形状。
# 设置用于绘图的网格
xx, yy = np.meshgrid(np.linspace(-7, 7, 150), np.linspace(-7, 7, 150))
# 创建绘图窗口
plt.figure(figsize=(len(anomaly_algorithms) * 2 + 4, 12.5))
plt.subplots_adjust(left=0.02, right=0.98, bottom=0.001, top=0.96, wspace=0.05, hspace=0.01)
plot_num = 1
rng = np.random.RandomState(42)
# 对每个数据集进行处理
for i_dataset, X in enumerate(datasets):
# 添加异常值
X = np.concatenate([X, rng.uniform(low=-6, high=6, size=(n_outliers, 2))], axis=0)
for name, algorithm in anomaly_algorithms:
t0 = time.time()
algorithm.fit(X)
t1 = time.time()
plt.subplot(len(datasets), len(anomaly_algorithms), plot_num)
if i_dataset == 0:
plt.title(name, size=18)
# 对数据拟合并标记异常值
if name == "局部异常因子":
y_pred = algorithm.fit_predict(X)
else:
y_pred = algorithm.fit(X).predict(X)
# 绘制等高线和点
if name != "局部异常因子": # LOF没有实现predict方法
Z = algorithm.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors="black")
colors = np.array(["#377eb8", "#ff7f00"])
plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[(y_pred + 1) // 2])
plt.xlim(-7, 7)
plt.ylim(-7, 7)
plt.xticks(())
plt.yticks(())
plt.text(
0.99,
0.01,
("用时 %.2fs" % (t1 - t0)).lstrip("0"),
transform=plt.gca().transAxes,
size=15,
horizontalalignment="right"
)
plot_num += 1
plt.show()
完整源码
import time
import matplotlib.pyplot as plt
import numpy as np
from sklearn import svm
from sklearn.covariance import EllipticEnvelope
from sklearn.datasets import make_blobs, make_moons
from sklearn.ensemble import IsolationForest
from sklearn.kernel_approximation import Nystroem
from sklearn.linear_model import SGDOneClassSVM
from sklearn.neighbors import LocalOutlierFactor
from sklearn.pipeline import make_pipeline
# 设置matplotlib参数以支持中文显示
plt.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
# 示例设置
n_samples = 300 # 样本总数
outliers_fraction = 0.15 # 异常值比例
n_outliers = int(outliers_fraction * n_samples) # 异常值数量
n_inliers = n_samples - n_outliers # 正常值数量
# 定义用于比较的异常检测方法
anomaly_algorithms = [
("鲁棒协方差", EllipticEnvelope(contamination=outliers_fraction, random_state=42)),
("单类SVM", svm.OneClassSVM(nu=outliers_fraction, kernel="rbf", gamma=0.1)),
("单类SVM (SGD)", make_pipeline(
Nystroem(gamma=0.1, random_state=42, n_components=150),
SGDOneClassSVM(nu=outliers_fraction, shuffle=True, fit_intercept=True, random_state=42, tol=1e-6)
)),
("隔离森林", IsolationForest(contamination=outliers_fraction, random_state=42)),
("局部异常因子", LocalOutlierFactor(n_neighbors=35, contamination=outliers_fraction))
]
# 定义数据集
blobs_params = dict(random_state=0, n_samples=n_inliers, n_features=2)
datasets = [
make_blobs(centers=[[0, 0], [0, 0]], cluster_std=0.5, **blobs_params)[0],
make_blobs(centers=[[2, 2], [-2, -2]], cluster_std=[0.5, 0.5], **blobs_params)[0],
make_blobs(centers=[[2, 2], [-2, -2]], cluster_std=[1.5, 0.3], **blobs_params)[0],
4 * (make_moons(n_samples=n_samples, noise=0.05, random_state=0)[0] - np.array([0.5, 0.25])),
14 * (np.random.RandomState(42).rand(n_samples, 2) - 0.5)
]
# 设置用于绘图的网格
xx, yy = np.meshgrid(np.linspace(-7, 7, 150), np.linspace(-7, 7, 150))
# 创建绘图窗口
plt.figure(figsize=(len(anomaly_algorithms) * 2 + 4, 12.5))
plt.subplots_adjust(left=0.02, right=0.98, bottom=0.001, top=0.96, wspace=0.05, hspace=0.01)
plot_num = 1
rng = np.random.RandomState(42)
# 对每个数据集进行处理
for i_dataset, X in enumerate(datasets):
# 添加异常值
X = np.concatenate([X, rng.uniform(low=-6, high=6, size=(n_outliers, 2))], axis=0)
for name, algorithm in anomaly_algorithms:
t0 = time.time()
algorithm.fit(X)
t1 = time.time()
plt.subplot(len(datasets), len(anomaly_algorithms), plot_num)
if i_dataset == 0:
plt.title(name, size=18)
# 对数据拟合并标记异常值
if name == "局部异常因子":
y_pred = algorithm.fit_predict(X)
else:
y_pred = algorithm.fit(X).predict(X)
# 绘制等高线和点
if name != "局部异常因子": # LOF没有实现predict方法
Z = algorithm.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors="black")
colors = np.array(["#377eb8", "#ff7f00"])
plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[(y_pred + 1) // 2])
plt.xlim(-7, 7)
plt.ylim(-7, 7)
plt.xticks(())
plt.yticks(())
plt.text(
0.99,
0.01,
("用时 %.2fs" % (t1 - t0)).lstrip("0"),
transform=plt.gca().transAxes,
size=15,
horizontalalignment="right"
)
plot_num += 1
plt.show()